Sololearn 自学机器学习(6)分类 Classification
分类在机器学习中属于哪一个部分
机器学习的顶层是由监督学习和无监督学习所组成的。分类在一个较高层次上属于监督学习的一部分。
监督学习是指我们将用一组有标记的历史数据来训练我们的模型。我们称那个标签(Label)或我们试图预测的事物为目标(Target)。因此,在监督学习中,历史数据有一个已知的目标,而在无监督学习中没有已知的目标。
在监督学习中,有分类(Classification)和回归(Regression)两种。分类问题是目标是分类值的情况(通常是True或False,但也可以是多个类别)。回归问题是目标是数值的情况。
例如,预测房价是一个回归问题。
- 它是属于监督学习的一种,因为我们有过去房屋销售的历史数据。
- 它是回归问题,因为房价是一个数值。
预测某人是否会违约是一个分类问题。
- 同样,它是监督学习,因为我们有过去借款人是否违约的历史数据,
- 它是一个分类问题,因为我们试图预测贷款是否属于两个类别之一(违约或不违约)。
逻辑回归(Logic Regression)虽然在其名称中包含“回归”,但是是用于解决分类问题的算法,而不是回归问题。
分类 Classification 术语 Terminology
让我们回顾一下我们的泰坦尼克号数据集。这是该数据集的 Pandas DataFrame:
Survived Pclass Sex Age Siblings/Spouses Parents/Children Fare |
Survived 列是我们试图预测的内容。我们称之为目标(Target)。你可以看到它是一个由 1 和 0 组成的列表。1 表示乘客幸存,0 表示乘客未幸存。
其余的列是关于我们可以用来预测目标的乘客的信息。我们称这些列中的每一列为特征(Features)。特征是我们用来进行预测的数据。
虽然我们知道数据集中的每个乘客是否幸存,但我们希望能够对我们无法收集到其数据的其他乘客进行预测。我们将构建一个机器学习模型来帮助我们做到这一点。
有时你会听到把特征称为预测变量 predictors。
线性分类模型
在机器学习中,线性模型是一种常见的分类方法。
让我们简要了解线性分类模型(内容涉及数学,慎重展开)
线性分类模型的基本思想是通过一个线性方程对输入特征进行加权求和,然后通过一个阈值函数(也称为激活函数)将结果映射到类别标签。这个线性方程的输出表示输入特征属于某个类别的程度。
数学上,给定输入特征向量 $X = [X_1, X_2, …, X_n]$,线性分类模型的输出 $y$ 计算如下:
$y = b + w_1X_1 + w_2X_2 + … + w_nX_n$
其中,$b$ 是偏置项(截距),$w_1, w_2, …, w_n$ 是权重,控制每个特征在分类中的影响程度。
然后,通过将输出 $y$ 输入激活函数,将连续的输出映射到类别标签。一种常用的激活函数是sigmoid函数,其数学表达式为:
$f(y) = \frac{1}{1 + e^{-y}}$
在二分类问题中,如果 $f(y) > 0.5$,则模型预测为正类别 $1$,否则预测为负类别 $0$。
这是一个简单的线性分类模型的概述。实际中,机器学习模型通常通过训练数据来学习最优的权重和偏置项,以便能够进行准确的分类。
图形化的分类
在项目的最终,我们将会用到 titanic.csv 中的所有特征值,但为了简单介绍,先使用其中两个特征(Fare 和 Age)这两种特征可以帮助我们在图表中可视化数据。
我们将乘客票价(Fare)绘制在 X 轴上,然后将其年龄绘制在 Y 轴上。黄色点是幸存乘客,紫色电视未幸存乘客。这个图的代码如下:
plt.scatter(df['Fare'], df['Age'], c=df['Survived']) |
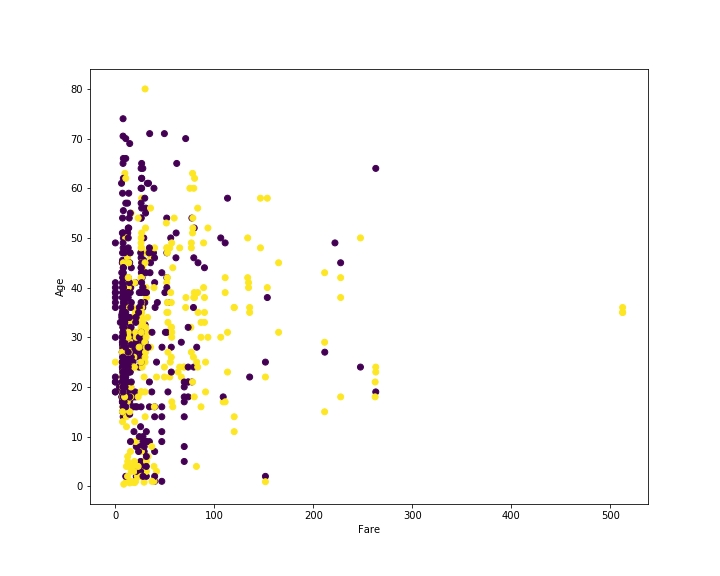
你可以看到在图的底部有更多的黄色点,而在顶部有更多的紫色点。这是因为儿童比成年人更有可能幸存,这符合我们的直觉。同样,在图的右侧有更多的黄色点,意味着支付更多的人更有可能幸存。
线性模型的任务是找到最好地将两个类别分开的线,使得黄色点在一侧,紫色点在另一侧。
下面是一个好的示例。该线用于对新乘客进行预测。如果乘客的数据点位于线的右侧,我们会预测他们会幸存。如果在左侧,我们会预测他们未幸存。
这条线是根据直觉给的,不要盲目跟风。
plt.scatter(df['Fare'], df['Age'], c=df['Survived']) |
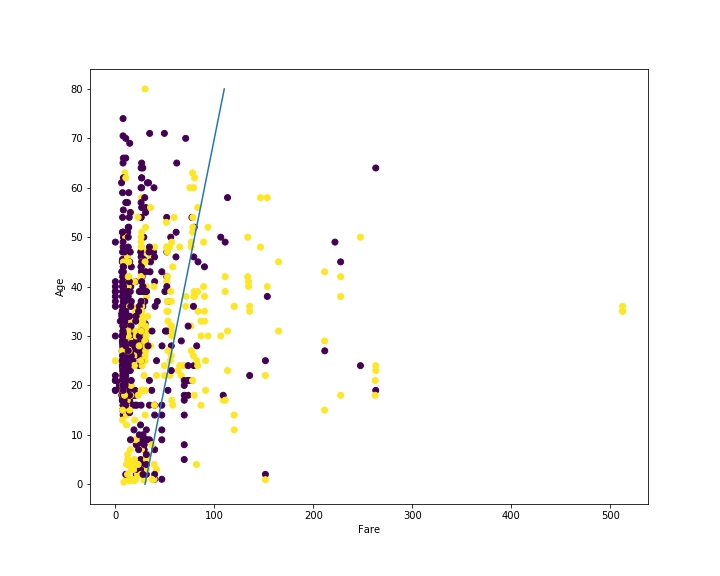
建立模型的挑战在于确定最佳的分隔线是什么。
线的方程式
线的方程可以用以下形式表示:
其中,a、b 和 c 是系数。任意三个值都将定义一条唯一的直线。
让我们看一个具体的例子,其中系数是 a=1,b=-1,c=-30。
三个系数分别是:1,-1,-30
回想一下,我们一直在用 x 轴表示乘客的票价(Fare),y 轴表示乘客的年龄(Age)。
为了画出方程表示的直线,我们需要两个位于直线上的点。
我们可以看到,例如点 (30, 0) 正好位于该直线上(票价 30,年龄 0)。如果我们将它代入方程,计算结果如下:
我们还可以看到,点 (50, 20) 位于该直线上(票价 50,年龄 20)。
以下是我们的直线在图上的样子。

直线的系数控制着直线的位置。
对线性方程式的讨论
另一种表示直线的方式
另一种表示直线的方式是:
在这里,$m$ 是直线的“斜率”;
$\theta$ 是直线与正 x 轴之间的角度。简而言之,$m$ 是一个数字,表示直线的倾斜程度。$\theta$ 表示水平,无穷大表示垂直,1 表示角度为 45° 或与两个轴(x 和 y)均匀倾斜。在 0 和无穷大之间的任何其他数字将直接与角度成正比(值越大,角度越大)。因此,正值 => 正角 => 逆时针旋转。负值将使直线顺时针旋转(值越负,角度越负)。
$c$ 是斜率,或直线与 y 轴相交的点的 y 坐标(当 $x = 0$ 时)。这种直线方程的形式可以帮助并减少确定所需直线方程所需的尝试次数。您只需要大致了解直线会倾斜多少(或与 x 轴成什么角度 $\theta$),使用计算器计算 $\tan \theta$ 并将得到的值放入 $m$ 的位置即可。
基于直线的预测
一个点位于直线的哪一侧决定了我们是否认为该乘客会幸存。
让我们再次看看同一条直线。

如果我们有一个乘客的数据,我们可以使用这个方程来确定他们在直线的哪一侧。例如,假设我们有一个票价为 100,年龄为 20 的乘客。
让我们将这些值代入我们的方程:
由于这个值是正的,该点位于直线的右侧,我们会预测该乘客幸存。
现在假设一个乘客的票价是 10,年龄是 50。让我们将这些值代入方程。
由于这个值是负的,该点位于直线的左侧,我们会预测该乘客未幸存。
我们可以在下面的图中看到这两个点。
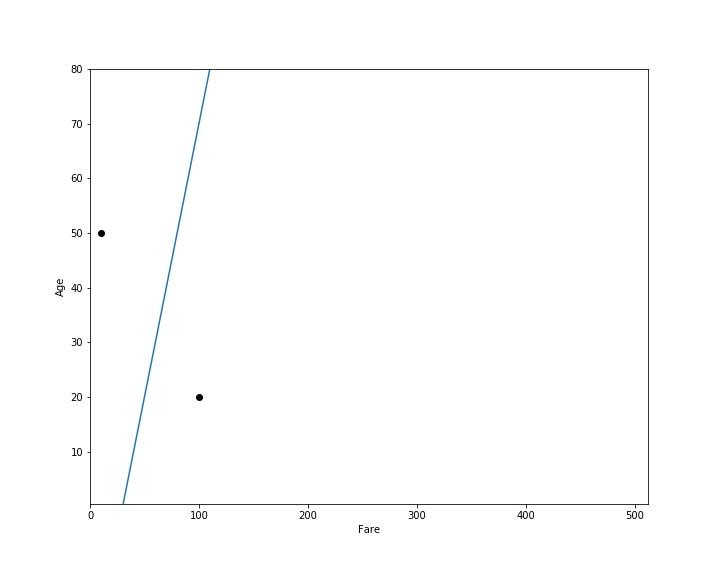
什么是一条好的直线?
让我们来看看两条不同的直线,首先是我们一直在使用的那条直线:我们称为直线 1

接下来是我们定义的另外一条直线方程,我们称之为直线 2
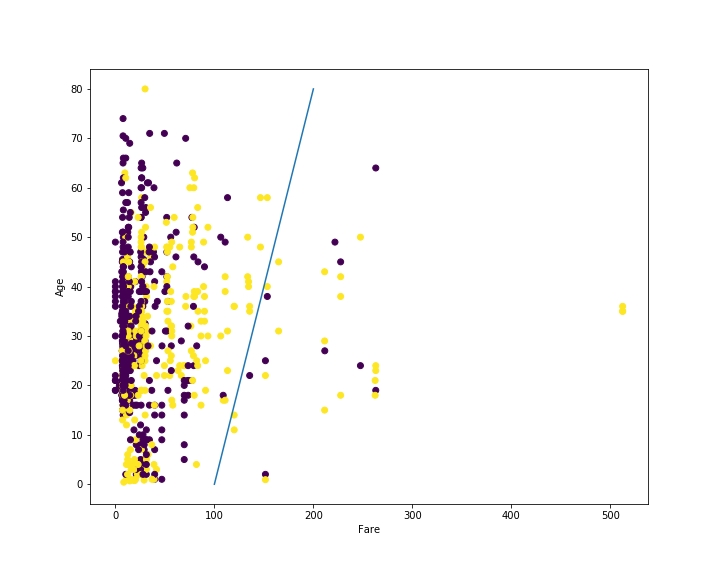
如果我们看这两条直线,我们会发现直线 1 在右侧有更多的黄色点,左侧有更多的紫色点。直线 2 在右侧没有太多点;大多数紫色和黄色点都在左侧。这使直线 1 成为更好的选择,因为它更好地分离了黄色和紫色点。
我们需要在数学上定义这个想法,以便我们可以通过算法找到最佳的直线。
逻辑回归是一种数学方法,可以找到最佳的直线。












