在分类任务中，两个常用的指标是精确度（precision）和召回率（recall）。从概念上讲，精确度指的是正确的正类别结果在所有模型预测的正类别结果中所占的百分比，而召回率指的是正确预测的正类别结果在所有实际正类别样本中所占的百分比。

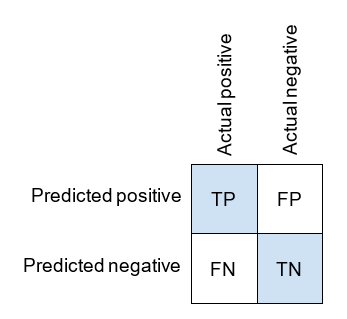
这两者都可以使用混淆矩阵中的象限来定义，而混淆矩阵如下：

英文原文

Two commonly used metrics for classification are precision and recall. Conceptually, precision refers to the percentage of positive results which are relevant and recall to the percentage of positive cases correctly classified.

Both can be defined using quadrants from the confusion matrix, which we recall is as follows:

精确度（Precision）

精确度是模型正确预测的正类别结果在所有模型预测的正类别结果中所占的百分比。其定义如下：

$\begin{aligned} \text{精确度} &= \frac{\text{正确预测的正类别数量}}{\text{模型预测的正类别总数量}} \\ &= \frac{\text{TP}}{\text{TP + FP}} \end{aligned}$

查看英文公式

$\begin{aligned} \text{precision} &= \frac{\text{nums of positives predicted correctly}}{\text{nums of positives predictions}} \\ &= \frac{\text{TP}}{\text{TP + FP}} \end{aligned}$

如果我们查看泰坦尼克号数据集上模型的混淆矩阵，我们可以计算精确度。

$\begin{aligned} \text{精确度} &= \frac{233}{(233 + 65)} \\ &= 0.7819 \end{aligned}$

Precision is a measure of how precise the model is with its positive predictions.

精确度是模型在其正类别预测中的准确性度量。

精确度的练习

我们的混淆矩阵如下所示。

	实际正类别	实际负类别
预测为正类别	30	20
预测为负类别	10	40

精确度是多少？0.6

查看解释

$\begin{aligned} \text{精确度} &= \frac{\text{正确预测的正类别数量}}{\text{模型预测的正类别总数量}} \\ &= \frac{\text{TP}}{\text{TP + FP}} \\ &= \frac{\text{30}}{\text{30 + 20}} \\ &= 0.6 \end{aligned}$

召回率（Recall）

召回率是模型正确预测的正类别占所有实际正类别样本的百分比。同样，我们将使用混淆矩阵来计算结果。

在这里，我们用数学方式定义召回率：

$\begin{aligned} \text{召回率} &= \frac{\text{正确预测的正类别数量}}{\text{正类别的数量}} \\ &= \frac{\text{TP}}{\text{TP + FN}} \end{aligned}$

查看英文公式

$\begin{aligned} \text{precision} &= \frac{\text{nums of positives predicted correctly}}{\text{nums of positives cases}} \\ &= \frac{\text{TP}}{\text{TP + FN}} \end{aligned}$

让我们计算泰坦尼克号数据集上模型的召回率。

$\begin{aligned} \text{召回率} &= \frac{233}{233 + 109} \\ &= 0.6813 \end{aligned}$

Recall is a measure of how many of the positive cases the model can recall.

召回率是模型能够检索多少正类别案例的度量。

召回率的练习

我们的混淆矩阵如下所示。

	实际正类别	实际负类别
预测为正类别	30	20
预测为负类别	10	40

召回率是多少？0.75

查看解释

$\begin{aligned} \text{召回率} &= \frac{\text{正确预测的正类别数量}}{\text{正类别的数量}} \\ &= \frac{\text{TP}}{\text{TP + FN}} \\ &= \frac{\text{30}}{\text{30 + 10}} \\ &= 0.75 \end{aligned}$

精确度和召回率的权衡（Trade-off）

英文原文

We often will be in a situation of choosing between increasing the recall (while lowering the precision) or increasing the precision (and lowering the recall). It will depend on the situation which we’ll want to maximize.

For example, let’s say we’re building a model to predict if a credit card charge is fraudulent. The positive cases for our model are fraudulent charges and the negative cases are legitimate charges.

Let’s consider two scenarios:

If we predict the charge is fraudulent, we’ll reject the charge.
If we predict the charge is fraudulent, we’ll call the customer to confirm the charge.

In case 1, it’s a huge inconvenience for the customer when the model predicts fraud incorrectly (a false positive). In case 2, a false positive is a minor inconvenience for the customer.

The higher the false positives, the lower the precision. Because of the high cost to false positives in the first case, it would be worth having a low recall in order to have a very high precision. In case 2, you would want more of a balance between precision and recall.

There’s no hard and fast rule on what values of precision and recall you’re shooting for. It always depends on the dataset and the application.

我们经常会面临在增加召回率（降低精确度）或增加精确度（降低召回率）之间进行选择的情况。我们选择哪个取决于我们希望最大化哪个度量，具体取决于情况。

例如，假设我们正在构建一个模型来预测信用卡交易是否存在欺诈。模型的正类别是欺诈交易，负类别是合法交易。

让我们考虑两种情况：

如果我们预测交易是欺诈的，我们将拒绝交易。
如果我们预测交易是欺诈的，我们将致电客户以确认交易。

在情况 1 中，当模型错误地预测欺诈（假正例）时，对客户来说是巨大的不便。在情况 2 中，假正例对客户来说只是轻微的不便。

假正例越多，精确度就越低。由于在情况 1 中假正例的代价很高，因此牺牲召回率以获得非常高的精确度可能是值得的。在情况 2 中，你可能希望在精确度和召回率之间取得更好的平衡。

在精确度和召回率方面，没有硬性规则确定你要追求的数值。这始终取决于数据集和应用场景。

精确度和召回率的权衡的练习

我们正在构建一个用于预测垃圾邮件的模型。正类别是垃圾邮件，负类别是合法邮件。如果我们要删除我们预测为垃圾邮件的电子邮件，那么在精确度和召回率中，哪一个更重要需要最大化？精确度（Precision）

查看解释

在这种情况下，最大化精确度（通过提高精确度）是很重要的；因为假正例将被删除（即被我们的模型错误预测为垃圾邮件的电子邮件），这可能导致重要的电子邮件被删除，因为出现了错误的预测。在这里，假正例的代价很高。因此，我们最好将其最小化（通过提高精确度）。

众所周知，垃圾邮件相较于合法（重要）邮件要少得多。

$\begin{aligned} \text{Precision} &= \frac{\text{TP}}{\text{TP + FP}} \\ \text{Recall} &= \frac{\text{TP}}{\text{TP + FN}} , \text{FP} > \text{FN} , \text{TP + FP} > \text{TP + FN} \\ \end{aligned}$ $\therefore \text{Precision} < \text{Recall} \\$

在这种情况下，最大化精确度（通过增加精确度）是很重要的，因为假正例（邮件被错误预测为垃圾邮件）会导致合法（重要）邮件被错误地“删除”。FP 的代价大于 FN，我们必须最大化精确度。

$\text{Maximize Precision:} \quad \text{Precision} = \frac{\text{TP}}{\text{TP + FP}}$

精确度和召回率的小结

更简单的定义：

Precision（精确度）：预测为正类别且实际上是正类别的数据点所占的百分比。即，所有正确预测为正类别（TP）占所有模型预测为
Recall（召回率）：实际为正类别且被模型正确预测为正类别的数据点所占的百分比。即，所有正确预测为正类别（TP）占所有实际正类别的数据点（TP + FN）的百分比。

F1 分数

准确率是一个吸引人的指标，因为它是一个单一的数字。精确度和召回率是两个数字，因此在两个模型之间选择时，如果一个模型的精确度较高，另一个模型的召回率较高，并不总是很明显该选择哪个。F1 分数是精确度和召回率的平均值，因此我们有一个单一的得分用于评估模型。

以下是F1分数的数学公式：

$\text{F1} = 2 \times \frac{\text{精确度 \times 召回率}}{\text{精确度 + 召回率}}$

让我们来计算泰坦尼克号数据集上模型的 F1 分数。我们将使用之前我们计算出来精确度和召回率的数值。精确度为 0.7819，召回率为 0.6813。F1 分数计算如下：

$\begin{aligned} \text{F1} &= 2 \times \frac{0.7819 \times 0.6813}{0.7819 + 0.6813} \\ &= 0.7281 \end{aligned}$

F1 分数是精确度和召回率值的调和平均（harmonic mean）。

衍生资料

如果精确度或召回率中的任一个较低，F1（调和平均）将比算术平均或几何平均更为敏感：

算术平均值：AM = $\frac{0.9 + 0.4}{2} = 0.65$
几何平均值：GM = $\sqrt{0.9 \times 0.4} \approx 0.6$
调和平均值：HM = $\frac{2 \times (0.9 \times 0.4)}{0.9 + 0.4} \approx 0.55$ 。

调和平均值比算术平均值更严厉地惩罚极端值，因此在需要考虑精确度和召回率，并且希望达到平衡性能的情况下，它是更为合适的选择。它在一个指标明显低于另一个指标的情况下特别有用。

两个值的调和平均在原始公式中为：

$\begin{aligned} HM &= \frac{2}{\left(\frac{1}{a} + \frac{1}{b}\right)} \\ &= \frac{2 \times 1}{\frac{(a + b)}{ab}} \\ &= \frac{2 \times ab}{(a + b)} \end{aligned}$

对于n个变量，我们将n除以分数之和 $\frac{1}{x}$：

$HM = \frac{n}{\left(\frac{1}{x_1} + \ldots + \frac{1}{x_n}\right)}$

还有其他一些均值：算术平均：

$AM = \frac{(x_1 + \ldots + x_n)}{n}$

几何平均：值的乘积的n次方根：

$GM = \sqrt[n]{x_1 \times \ldots \times x_n}$

因此，有趣的一点是对于非负值总是成立的：$ AM \geq GM \geq HM $，只有当所有值相同时才会达到相等。简而言之，调和平均更接近较小的值，因此F1试图保持最小值较高。