Sololearn 自学机器学习（10）模型评估

“Model Evaluation” 的意思是对模型进行评估，即检查和量化模型在给定数据集上的性能和效果的过程。在机器学习中，构建一个模型后，我们通常需要评估它的性能，以确保其在实际应用中表现良好。

模型评估的目的是了解模型在预测新数据时的准确性、稳健性和可靠性。一些常见的模型评估指标包括准确率、精确度、召回率、F1 分数等，这些指标提供了关于模型在不同方面表现的信息。

总体而言，模型评估是机器学习中至关重要的一步，帮助我们了解模型在特定任务上的表现，从而可以进行调整、改进或选择其他模型。

准确率（Accuracy）

在前面的模块中，我们使用准确率（Accuracy）来衡量模型的性能。准确率是正确预测的百分比。

如果你有100个数据点，其中70个被正确预测，30个被错误预测，那么准确率为70%。

准确率是一个非常直观且易于理解的指标，但并不总是最好的指标。例如，假设我有一个模型用于预测信用卡交易是否存在欺诈。在 10000 笔信用卡交易中，有 9900 笔是合法交易，100 笔是欺诈交易。我可以构建一个模型，只是预测每一笔交易都是合法的，这样它就会在预测中获得 9900/10000（99%）的准确率！

对于欺诈信用卡活动的例子属于不平衡的数据集。在收集信用卡活动数据时，大部分活动将是合法的，而找到欺诈活动的实例相对较难。这是一个问题，因为通常我们更关心预测少数类别的情况，或者在这种情况下是欺诈活动。

处理不平衡数据集有一些策略。我们可以过采样少数类别。在我们的例子中，这意味着我们会在数据集中包含每个欺诈活动案例99次。这样做可以平衡数据中每个活动类别的表示。

或者，我们可以更重视预测欺诈活动的错误，而不是预测合法活动的错误。通过谷歌搜索，你可以找到更多处理不平衡数据集的想法。

如果我们的类别平均分布，准确率是一个很好的度量，但如果类别不平衡，它就会非常误导。

在使用准确率时要谨慎。你需要了解类别的分布情况，以了解如何解释这个值。

对于准确率的练习

假设你的任务是构建一个模型来预测垃圾邮件。你的训练集有 1000 封电子邮件，其中 950 封是合法邮件，50 封是垃圾邮件。你构建了一个模型，只是预测每封电子邮件都是合法的。这个模型的准确率是多少？查看答案 95%

混淆矩阵（Confusion Matrix）

正如我们在前面部分中注意到的，我们不仅关心我们正确预测了多少数据点的类别，还关心我们正确预测了多少正类别数据点以及我们正确预测了多少负类别数据点。

我们可以在所谓的混淆矩阵 (Confusion Matrix)（或错误矩阵 (Error Matrix) 或混淆表 (Table of Confusion)）中看到所有重要的值。

混淆矩阵是一个显示四个值的表格：

• 我们预测为正类别且实际上是正类别的数据点
• 我们预测为正类别但实际上是负类别的数据点
• 我们预测为负类别但实际上是正类别的数据点
• 我们预测为负类别且实际上是负类别的数据点

第一和第四个是我们正确预测的数据点，而第二和第三个是我们错误预测的数据点。

在我们的泰坦尼克号数据集中，有887名乘客，342名幸存（正类别）和545名未幸存（负类别）。我们在前一模块中构建的模型具有以下混淆矩阵。

蓝色阴影的方块是我们正确预测的预测次数。因此，在 342 名幸存的乘客中，我们正确预测了 233 人（错误预测了 109 人）。在 545 名未幸存的乘客中，我们正确预测了 480 人（错误预测了 65 人）。

我们可以使用混淆矩阵来计算准确率。作为提醒，准确率是正确预测的数据点数量除以总数据点数量。

$$\begin{aligned} \text{准确率} &= \frac{\text{主对角线元素之和}}{\text{所有元素之和}} \\ \frac{(233 + 480)}{(233 + 65 + 109 + 480)} &= \frac{713}{887} \\ &= 80.38\% \end{aligned}$$

这确实是我们在前一模块中得到的相同值。（注：在逻辑回归中，我们使用的是另一个源的模型数据，所以概率在 79% 左右。

混淆举证完全描述了模型在数据集上的性能，景观他难以用于比较模型。

混淆矩阵的练习

根据下面的混淆矩阵，计算模型的准确率。

	实际正类别	实际负类别
预测为正类别	20	26
预测为负类别	10	44

准确率将是多少？查看答案 64%

查看解释

计算矩阵的主对角线上的元素之和，然后除以矩阵所有元素的和。

$$\begin{aligned} \frac{(20 + 44)}{(20 + 26 + 10 + 44)} &= \frac{64}{100} \\ &= 64\% \end{aligned}$$

真正例、真负例、假正例、假负例

对于混淆矩阵的每个方格，我们有相应的术语。

真正例（True Positive，TP） 是我们正确预测为正类别的数据点。
真负例（True Negative，TN） 是我们正确预测为负类别的数据点。
假正例（False Positive，FP） 是我们错误地预测为正类别的数据点。
假负例（False Negative，FN） 是我们错误地预测为负类别的数据点。

这些术语可能有点难以记住。记住的方法是，第二个词表示我们的预测是什么（正类别或负类别），而第一个词表示该预测是否正确（真或假）。

通常会看到混淆矩阵描述如下：

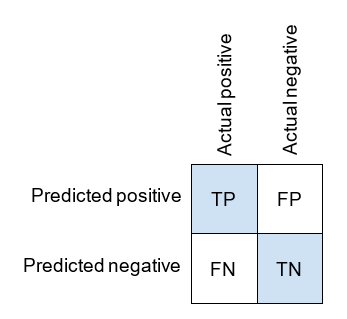
混淆矩阵的四个值（TP、TN、FP、FN）用于计算后面将要使用的几个不同的度量指标。

真假正负例的练习

	实际正类别	实际负类别
预测为正类别	233	65
预测为负类别	109	480

• 那里有 233 个 查看答案 真正例（True Positive）
• 那里有 65 个 查看答案 假正例（False Positive）
• 那里有 109 个 查看答案 假负例（False Negative）
• 那里有 480 个 查看答案 真负例（True Negative）