受试者工作特征（ROC）曲线是模型区分正类和负类的能力在不同阈值下的图形表示。在深入研究ROC曲线之前，有一些基本概念需要了解：

真正例（TP）： 模型正确预测正实例。
假正例（FP）： 模型错误地预测正实例（Type I 错误）。
真负例（TN）： 模型正确预测负实例。
假负例（FN）： 模型错误地预测负实例（Type II 错误）。
灵敏度（真正例率或召回率）： 它是正确预测的正实例与总实际正实例的比率。它量化了模型捕获正实例的能力。灵敏度 = TP / (TP + FN)。
特异性（真负例率）： 它是正确预测的负实例与总实际负实例的比率。它量化了模型捕获负实例的能力。特异性 = TN / (TN + FP)。
精确度（正预测值）： 它是正确预测的正实例与总预测正实例的比率。精确度 = TP / (TP + FP)。
假正例率（FPR）： 它是错误地预测的正实例与总实际负实例的比率。FPR = FP / (FP + TN)。

这些概念对于理解ROC曲线非常重要，ROC曲线可视化了在不同分类阈值下灵敏度和特异性之间的权衡。

逻辑回归阈值 (Logistic Regression Threshold)

如果你回忆一下第 11 话，我们讨论了精确度 (Precision) 和召回率 (Recall) 之间的权衡。对于 Logistic Regression 模型，我们有一种简单的方法在强调精确度和强调召回率之间进行切换。Logistic Regression 模型不仅返回一个预测值，而且返回一个介于 0 到 1 之间的概率值。通常，我们说如果这个值 >= 0.5，我们预测乘客幸存，如果这个值 < 0.5，乘客就没有幸存。然而，我们可以选择任何介于 0 到 1 之间的阈值。

如果我们将阈值设得更高，我们将有更少的正预测，但我们的正预测更有可能是正确的。这意味着精确度会更高，而召回率会更低。
如果我们将阈值设得更低，我们将有更多的正预测，因此更有可能捕捉到所有的正例。这意味着召回率会更高，而精确度会更低。

每个阈值的选择都是一个不同的模型。ROC (Receiver operating characteristic, 受试者工作特征) 曲线 (Curve) 是一个显示所有可能模型及其性能的图形。

ROC 的历史

它首次在二战期间被用于分析雷达信号，以更好地检测敌机与信号噪声（如大群的鹅）之间的区别。特别是，他们使用了我们在机器学习中将要学习和使用的同一种数学，用于评估雷达接收器操作员做出重要区分的能力，比如刚刚在雷达上观察到的是敌机目标、友方船只还是噪声。因此，这就是接收器工作特征（ROC, receiver operating characteristic）的名字的由来。这个非常数学 (very math) 的理论随后被归类为“信号检测理论 (signal detection theory) ”。你可能已经听说过医学检测中的“假阳性率 (false positive rate) ”这个术语。

灵敏度 (Sensitivity) 和特异性 (Specificity)

ROC 曲线是灵敏度与特异性之间的图形。这些值展示了与精确度和召回率相同的权衡。

让我们回顾混淆矩阵，因为我们将使用它来定义灵敏度和特异性。

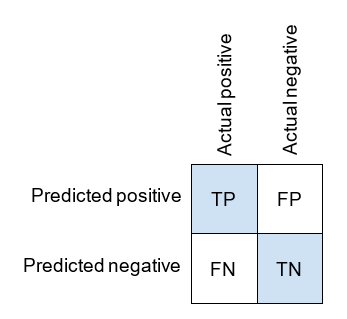
灵敏度 (Sensitivity) 是召回率的另一种术语，即真正例率 (True positive rate) 。回忆一下，它的计算方法如下：

$\begin{aligned} \text{灵敏度} = \text{召回率} &= \frac{\text{正确预测的正类别数量}}{\text{正类别的数量}} \\ &= \frac{\text{TP}}{\text{TP + FN}} \end{aligned}$

特异性 (Specificity) 是真负例率。它的计算方法如下。

$\begin{aligned} \text{特异性} = \text{召回率} &= \frac{\text{正确预测的负类别数量}}{\text{负类别的数量}} \\ &= \frac{\text{TN}}{\text{TN + FP}} \end{aligned}$

我们在 Titanic 数据集上进行了训练集和测试集的拆分，并得到了以下混淆矩阵。在我们的测试集中，有 96 个正例和 126 个负例。

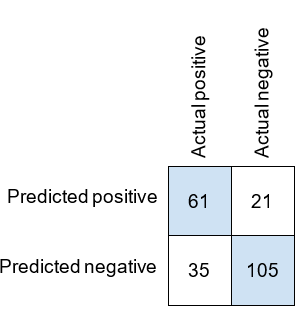
让我们计算灵敏度和特异性。

$\begin{aligned} \text{灵敏度} & = \frac{61}{96} \approx 0.6354 \\ \text{特异性} & = \frac{105}{126} \approx 0.8333 \\ \end{aligned}$

目标是最大化这两个值，尽管通常使一个值变大会使另一个值变小。更注重敏感性还是特异性，要根据具体情况而定。

虽然我们通常查看精确度和召回率的值，但绘制图表的标准是使用敏感性和特异性。虽然也可以构建精确度 - 召回率曲线，但这并不常见。

灵敏度和特异性的练习

从以下混淆矩阵中，灵敏度和特异性分别是多少？

预测 \ 实际	实际正例	实际负例
预测正例	30	20
预测负例	10	40

查看答案

计算：

$\begin{aligned} 灵敏度（召回率）&= \frac{\text{正确预测的正例}}{\text{实际正例数}} \\ &= \frac{30}{30 + 10} \\ &= 0.75 \\ \\ 特异性 &= \frac{\text{正确预测的负例}}{\text{实际负例数}} \\ &= \frac{40}{40 + 20} \\ &= 0.67 \end{aligned}$

灵敏度（召回率）= 正确预测的正例 / 实际正例数 = 30 / (30 + 10) = 0.75

特异性 = 正确预测的负例 / 实际负例数 = 40 / (40 + 20) = 0.67

因此，灵敏度为 0.75，特异性为 0.67。

Sklearn 中的灵敏度和特异性

在Scikit-learn中，虽然没有专门定义灵敏度（Sensitivity）和特异性（Specificity）的函数，但我们可以自己定义。由于灵敏度与召回率相同，所以定义起来很容易。

from sklearn.metrics import recall_score
sensitivity_score = recall_score
print(sensitivity_score(y_test, y_pred)) 
# 0.6829268292682927

现在，要定义特异性，如果我们意识到它也是负类别的召回率，我们可以从sklearn的precision_recall_fscore_support函数中获取该值。

让我们看看precision_recall_fscore_support的输出。

from sklearn.metrics import precision_recall_fscore_support
print(precision_recall_fscore_support(y, y_pred))

输出的第二个数组是召回率，因此我们可以忽略其他三个数组。这个数组有两个值。第一个是负类别的召回率，第二个是正类别的召回率。第二个值是标准的召回率或灵敏度值，你可以看到该值与上面得到的值相匹配。第一个值是特异性。因此，让我们编写一个函数只获取该值。

def specificity_score(y_true, y_pred):
    p, r, f, s = precision_recall_fscore_support(y_true, y_pred)
    return r[0]
print(specificity_score(y_test, y_pred)) 
# 0.9214285714285714

请注意，在代码示例中，我们在训练测试拆分中使用了一个随机种子，以便每次运行代码时都能获得相同的结果。

import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import recall_score, precision_recall_fscore_support

sensitivity_score = recall_score
def specificity_score(y_true, y_pred):
    p, r, f, s = precision_recall_fscore_support(y_true, y_pred)
    return r[0]

df = pd.read_csv('https://kingsmai.github.io/uploads/@files/datasets/titanic/titanic.csv')
df['male'] = df['Sex'] == 'male'
X = df[['Pclass', 'male', 'Age', 'Siblings/Spouses', 'Parents/Children', 'Fare']].values
y = df['Survived'].values

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=5)

model = LogisticRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)

print("sensitivity:", sensitivity_score(y_test, y_pred))
print("specificity:", specificity_score(y_test, y_pred))

Sklearn 中的灵敏度和特异性的练习

以下代码会得到什么值？

p, r, f, s = precision_recall_fscore_support(y_test, y_pred)
print(r[1])

查看答案

这段代码将打印正类别的召回率（recall）。

r[0] 捕获的是特异性，r[1] 捕获的是灵敏度（标准召回率），但对于灵敏度，无需使用这个数组，因为Python中已经有了 recall_score() 方法用于计算正类别的值。

SkLearn 中调整逻辑回归阈值

在使用 scikit-learn 的 predict 方法时，会得到预测的 0 和 1 值。然而，在幕后，Logistic Regression 模型对于每个数据点都获得一个介于 0 到 1 之间的概率值，然后四舍五入为 0 或 1。如果我们想要选择除 0.5 之外的不同阈值，我们将需要这些概率值。我们可以使用 predict_proba 函数来获取它们。

model.predict_proba(X_test)

结果是一个包含每个数据点的 2 个值的 numpy 数组（例如，[0.78, 0.22]）。你会注意到这两个值的总和为 1。第一个值是数据点属于 0 类（未幸存）的概率，第二个是数据点属于 1 类（幸存）的概率。我们只需要该结果的第二列，可以使用以下 numpy 语法提取。

model.predict_proba(X_test)[:, 1]

现在，我们只需将这些概率值与我们的阈值进行比较。假设我们想要一个阈值为 0.75。我们将上面的数组与 0.75 进行比较。这将给我们一个包含 True/False 值的数组，这将是我们的预测目标值的数组。

y_pred = model.predict_proba(X_test)[:, 1] > 0.75

0.75 的阈值意味着我们需要更有信心才能进行正面预测。这导致较少的正面预测和更多的负面预测。

现在，我们可以使用之前的任何 scikit-learn 指标，使用 y_test 作为我们的真实值，y_pred 作为我们的预测值。

print("precision:", precision_score(y_test, y_pred))
print("recall:", recall_score(y_test, y_pred))

运行以下代码以查看结果。

import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import precision_score, recall_score
from sklearn.model_selection import train_test_split

df = pd.read_csv('https://kingsmai.github.io/uploads/@files/datasets/titanic/titanic.csv')
df['male'] = df['Sex'] == 'male'
X = df[['Pclass', 'male', 'Age', 'Siblings/Spouses', 'Parents/Children', 'Fare']].values
y = df['Survived'].values

X_train, X_test, y_train, y_test = train_test_split(X, y)

model = LogisticRegression()
model.fit(X_train, y_train)

y_pred = model.predict_proba(X_test)[:, 1] > 0.75

print("precision:", precision_score(y_test, y_pred))
print("recall:", recall_score(y_test, y_pred))

将阈值设置为 0.5 会得到原始的 Logistic Regression 模型。任何其他阈值都会产生一种替代模型。

对于 `predict_proba` 的补充

使用 predict_proba 方法既给出乘客死亡的概率，又给出乘客幸存的概率，可能会显得有些奇怪。毕竟，我们只需要其中一列，而通过从 1 中减去第一列，我们就可以得到另一列。在我们的情况下，我们只有两个类别（幸存和未幸存），但对于有两个以上目标类别的问题，获取所有可能类别的概率是非常有用的。