在机器学习的学习过程中，统计学是一个至关重要的基础知识。本章将对一些基础统计概念进行回顾，这些概念构成了机器学习理论和实践的基础。

平均数

平均数
在处理数据时，我们经常需要计算一些简单的统计量。

假设我们有一个班级学生年龄的列表，按升序排列以便更容易进行计算。

15, 16, 18, 19, 22, 24, 29, 30, 34

均值（Mean）是最常见的平均数。

将所有值相加，然后除以值的数量：

中位数（Median）是中间的值。在这种情况下，由于有9个值，中间值是第5个，即22。

在统计学中，均值和中位数都被称为平均数。在一般用语中，平均数通常指的是均值。

百分位数（Percentiles）

中位数也可以被视为第 50 个百分位数。这意味着 50% 的数据小于中位数，而 50% 的数据大于中位数。这告诉我们数据的中间位置在哪里，但我们通常希望更深入地了解数据的分布。我们经常会查看第 25 个百分位数和第 75 个百分位数。

第 25 个百分位数是数据的四分之一处的值。这是一个值，其中25%的数据小于它（而75%的数据大于它）。

同样，第 75 个百分位数是数据的四分之三处的值。这是一个值，其中75%的数据小于它（而25%的数据大于它）。

如果我们再看一下我们的年龄数据：

15, 16, 18, 19, 22, 24, 29, 30, 34

我们有9个值，因此数据的 25% 大约是 2 个数据点。因此，第 3 个数据点大于 25% 的数据。因此，第 25 个百分位数是 18（第 3 个数据点）。
同样，数据的75%大约是 6 个数据点。因此，第 7 个数据点大于75%的数据。因此，第 75 个百分位数是 29（第 7 个数据点）。

我们的数据的完整范围在 15 到 34 之间。第 25 和第 75 个百分位数告诉我们，我们的数据有一半位于 18 和 29 之间。这有助于我们了解数据的分布方式。

如果数据点的数量是偶数，为了找到中位数（或第50个百分位数），您需要取中间两个值的平均值。

百分位数练习

假设我们有一个包含 11 个家庭及每个家庭孩子数量的样本。列表中的每个数字代表一个家庭的孩子数量。因此，有 1 个家庭没有孩子，有 5 个家庭有 1 个孩子，依此类推。

0，1，1，1，1，1，2，2，2，3，6

第25个百分位数是 1

第50个百分位数（又称中位数）是 1

第75个百分位数是 2

标准差和方差

我们可以通过标准差（Standard Deviation）和方差（Variance）更深入地了解数据的分布。标准差和方差是衡量数据分散或扩散程度的指标。

我们测量每个数据点离均值的距离。

让我们再次看一下我们的年龄组：

15, 16, 18, 19, 22, 24, 29, 30, 34

回想一下均值是23。

让我们计算每个值离均值的距离。15 离均值 8 个单位（因为 23 - 15 = 8）。

以下是所有这些距离的列表：

8, 7, 5, 4, 1, 1, 6, 7, 11

我们对这些值进行平方并相加。

然后，我们将这个值除以总值的数量，得到方差。

要得到标准差，我们只需对方差取平方根，得到：6.34

If our data is normally distributed like the graph below, 68% of the population is within one standard deviation of the mean. In the graph, we’ve highlighted the area within one standard deviation of the mean. You can see that the shaded area is about two thirds (more precisely 68%) of the total area under the curve. If we assume that our data is normally distributed, we can say that 68% of the data is within 1 standard deviation of the mean.

如果我们的数据像下面的图表一样呈正态分布，那么 68% 的人口在均值的一个标准差内。在图表中，我们突出显示了均值一个标准差内的区域。您可以看到，阴影区域大约是曲线下总面积的三分之二（更精确地说是 68% ）。如果我们假设我们的数据正态分布，我们可以说 68% 的数据在均值的 1 个标准差内。

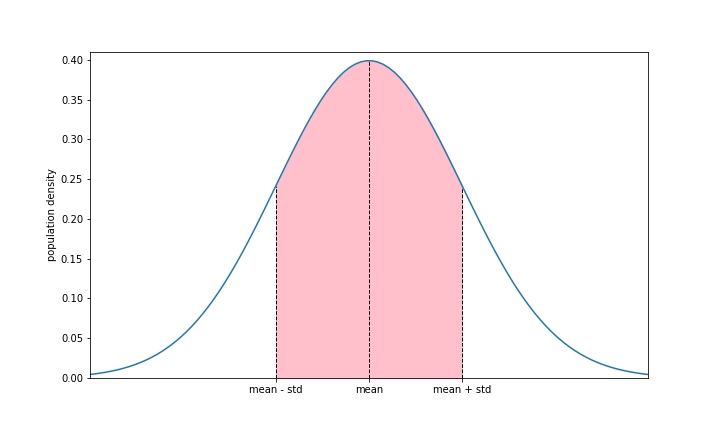
In our age example, while the ages are likely not exactly normally distributed, we assume that we are and say that approximately 68% of the population has an age within one standard deviation of the mean. Since the mean is 23 and the standard deviation is 6.34, we can say that approximately 68% of the ages in our population are between 16.66 (23 minus 6.34) and 29.34 (23 plus 6.34).

在我们的年龄示例中，虽然年龄可能不完全是正态分布的，但我们假设是，并说大约 68% 的人口在均值的一个标准差内具有年龄。由于均值是 23，标准差是 6.34，我们可以说大约 68% 的年龄在我们的人口中介于 16.66（23 减去 6.34）和 29.34（23 加上 6.34）之间。

即使数据永远不是完美的正态分布，我们仍然可以使用标准差来洞察数据的分布方式。

The standard deviation and variance are measures of how dispersed the data is.

使用 Python 进行统计学计算

我们可以使用 Python 计算所有这些操作。我们将使用 Python 包 numpy。稍后我们将更多地使用 numpy 来操作数组，但现在我们将仅使用其中一些用于统计计算的函数：mean（均值）、median（中位数）、percentile（百分位数）、std（标准差）、var（方差）。

首先，我们导入这个包。习惯上将 numpy 取一个别名为 np。

import numpy as np

让我们初始化变量data，将其赋值为年龄的列表。

data = [15, 16, 18, 19, 22, 24, 29, 30, 34]

现在我们可以使用 numpy 函数。对于mean（均值）、median（中位数）、standard deviation（标准差）和 variance（方差）函数，我们只需传入数据列表。对于 percentile（百分位数）函数，我们传入数据列表和百分位数（作为0到100之间的数字）。

import numpy as np

data = [15, 16, 18, 19, 22, 24, 29, 30, 34]

print("mean:", np.mean(data))
print("median:", np.median(data))
print("50th percentile (median):", np.percentile(data, 50))
print("25th percentile:", np.percentile(data, 25))
print("75th percentile:", np.percentile(data, 75))
print("standard deviation:", np.std(data))
print("variance:", np.var(data))

Numpy 是一个允许在数组上执行快速且轻松的数学运算的 Python 库。