什么是数字签名

在比特币的原理的文章里，我提到了数字签名这项技术。那这个数字签名是什么东西呢？它怎么去执行加密的？

生日碰撞

在讨论数字签名前，先来了解生日碰撞的概念。以下涉及概率论，我会尽量说的简单点。

问题：一个班级有50个学生，至少两个学生生日在同一天的概率是多少？可能很多人都会觉得，一年 365 天，这概率很低。但是真的是这样吗？举个实例：中学的时候，我班和我同一天生日的就有三个人。

那么这个概率怎么算呢？

首先，我定义 P = 所有人的生日不在同一天的概率，那么 1 - P = 至少两个人生日在同一天的概率。
如果全班只有 1 个人， P = 100%，因为 P = 365 / 365，一年有 365 天，他可以任选一天。
全班有两个人，那么 P = (365 / 365) × (364 / 365) ，第一个人任选一天后，第二个人只能从 365 天里的 364 天选其中一天。
以此类推，当全班有 n 个人，Pn = (365 × 364 × … × (365 - n + 1) ) / 365 n

当全班有 10 个人，则 P10 = 88.1%，也就是 88.3% 的概率全班不在同一天生日。而 1 - P = 11.7% 也就是 11.7% 的概率至少两个同学同一天生日。

当全班有 20 个人，则 P20 = 48.8% 而 1 - P = 51.2%。

而全班有 50 个人，则全班不在同一天生日的概率 P50 = 2.9% 反之 1 - P = 97.1%。

数字签名不是一种加密，和我们现实生活中的签名是一样的。在比特币的安全我们在讨论比特币安全性质的时候说到，电脑因为能轻易的保存并复制我们传统的身份认证（人脸、签名、指纹）。所以需要给数据加上一个电脑无法复制的电子签名。

哈希函数

这里就用到了一项技术——哈希函数。它可以给某个字符串（数据）经过计算之后，变为一个有限长度的新的字符串。我们将它生成出来的值称为摘要（digest）或散列值（hash values）。这个摘要就相当于数据的指纹。

举个栗子：
我将 123 经过哈希函数计算之后，得出一个 3 位的结果 abc；
而我将 4abd5 通过哈希函数计算之后，也能得出一个 3 位的结果 efg。
你给我一个长度为 10G 的电影，最后也得出一个 3 位的结果

而这个哈希函数具有不可逆（无法从摘要逆向演算回初值）的性质，所以可以用来加密密码。

所以我们知道了哈希函数的两个特点：

单向的——你给我摘要，问我源数据是什么，我不知道。
位数固定——不论多长的数据，经过哈希函数之后都会变成一个和其他数据一样长的结果。具体生成长度，取决于你所使用的哈希函数的类型。

因为最终生成结果是固定的，所以有可能会出现两个不同的数据最终得出同样结果的情况，这个情况称之为生日碰撞。而出现生日碰撞就达不到数字签名的要求了。因为签名是必须独一无二的。所以只能修改哈希函数的算法来降低生日碰撞。

经过计算，如果你的哈希值有 N 个，那么生日碰撞概率大于 50% 只需要 1.2 × √n 就行了。

如果哈希值有 100 种可能，那么出现生日碰撞大于 50% 的概率所需的原项只需要 12 个。
如果有 10000 种可能，则只需要 120 个原项。

数字签名的过程

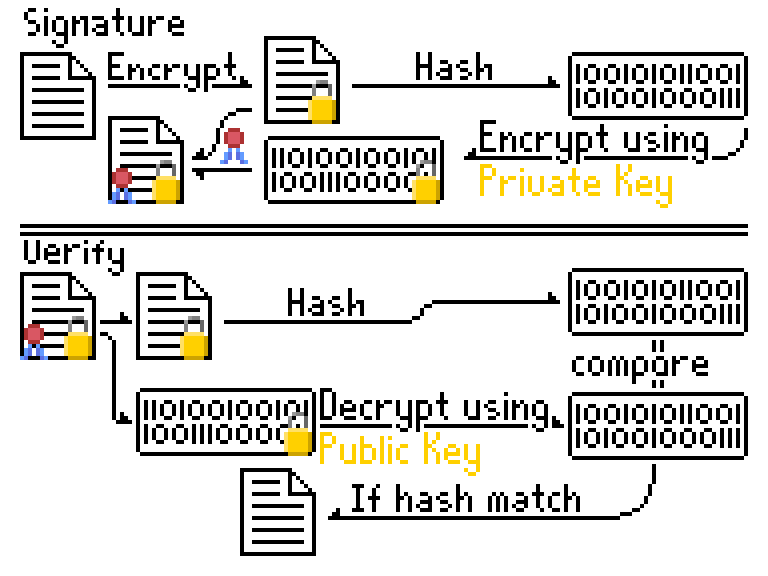
签名的目的是让别人知道这个信息是你发出来的。我们用非对称加密进行解释。

A 要给 B 发送一组数据。他要先把这组数据进行加密
1. 加密方法是公开的，谁都能加密
2. 只有 B 知道怎么解密。
然后 A 还需要把这组数据进行哈希运算之后，再通过私钥加密。使其成为数字签名。
1. 钥匙分了两把：私钥是 A 自己的钥匙，A 自己保存好，任何人都不知道，用于加密的。
2. 公钥是 A 公开给所有人的钥匙，用于解密由 A 加密的密文。
A 把加密后的数据连同数字签名一并发给 B
B 将加密后的数据进行哈希运算后，得到哈希值。再通过公钥解密，得到 A 加密的哈希值。
最后 B 比较两组哈希值，如果两组哈希值能对上，那么表示数据由 A 发出来，并且中途未被篡改。